"Какой он к черту проповедник! 

Он - мошенник и все врет!"

М. Твен.

"Приключения Гекльберри Финна".

,

,

.

:..Тем более, что первое из этих соотношений нам хорошо знакомо. Оно выражает собой свойство аддитивности массы.

:..Другими словами, аддитивность массы означает, что сложенные вместе десять одинаковых кирпичей будут обладать вдесятеро большей инертностью, нежели один кирпич. Если же нам удастся каким-то образом "соединить" кирпичи так, чтобы массы "опрокидывались вверх ногами", подобно емкостям последовательно соединенных конденсаторов, то инертность десяти кирпичей будет в десять раз меньше инертности одного кирпича. Иначе говоря, чем больше вы будете загружать вагон вашим способом, тем легче будет его везти! Уж не таким ли образом перемещали 200-тонные блоки древние строители храмовых комплексов в долине Гизы? В наше время в мире существует лишь несколько кранов, способных работать с 200-тонными грузами. А как древние инженеры собирались поднять, передвинуть и установить знаменитый гранитный "Незаконченный обелиск" из древних каменоломен вблизи Асуана? - Его высота 42 метра, а вес 1150 тонн. Обелиск потрескался при обработке, и его оставили на месте. Не по наивности же вырубили его из скалы, не зная, сумеют установить или нет. Дискуссии о способах перемещения подобных тяжестей в древние времена ведутся постоянно. Стоит, однако, отметить, что первоначальный вес "Гром-камня", послужившего основанием для знаменитого памятника Петру Первому в Петербурге, составлял 1800 тонн. А после обработки - около 1200 тонн.  Тем не менее, его переместили из Лахты в Петербург и по суше и по морю, для чего изобрели попутно кольцевой шарикоподшипник. И никаких "волшебных" способов не понадобилось.

     Вернемся, однако, к нашей идее об уменьшении инертности взаимодействующих масс.  Попробуйте придумать, как соединять тела, для того, чтобы последняя из приведенных выше двух формул стала соответствовать реальности. Это будет великое открытие, Нобелевская премия, прижизненная и посмертная слава.Наука такого способа соединения кирпичей не знает. И вряд ли он существует в Природе. Давайте на всякий случай протестируем этот гипотетический способ законами сохранения энергии и импульса. Пусть, по аналогии с задачей о неупругом столкновении двух тел массой m каждое, сталкиваются два таких же тела, соединяясь нашим фантастическим способом. При этом масса образовавшегося тела будет, естественно, m/2. Из закона сохранения импульса следует:

,

,

где

.

:..Итак, в первой нашей "нормальной" задаче о неупругом столкновении двух тел равной массы терялась ровно половина энергии. А в данном случае эта энергия должна выделяться. Еще бы! Ведь кинетическая энергия наших "ненормально" слипшихся тел тоже возросла вдвое. А откуда взяться этой дополнительной энергии? Вообще говоря, есть откуда. Ведь у нас в столкновении куда-то пропала масса, равная 3/2m . Согласно Эйнштейну, с массой связана энергия E = mc² , так что в нашем распоряжении E = 3/2 mc², что для кирпичей массой m = 5 кг составит фантастическую энергию в 6,75·10¹⁷джоулей (Дж). Итак, куда девается избыток энергии - непонятно. Словом, вся эта задача - сплошная фантастика! И действительно, нельзя так прямолинейно проводить аналогии между в чем-то схожими внешне, но в корне различающимися понятиями.

Тем не менее, выражение для массы тела, аналогичное искомому, в физике все же существует и называется оно "приведенной массой". Смысл его, однако, совершенно иной и заключается в том, что математически задача о движении во внешнем поле двух взаимодействующих материальных точек сводится к решению задачи о движении одной точки с массой равной

:::::                                  

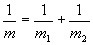
Подробнее с этим методом вы можете познакомиться в любом курсе "Механики" для высших учебных заведений.